Monday, 21 October 2013
Friday, 18 October 2013
T4 W2 Adding and Subtracting Decimals
Hi
Jaslyn, Danita, Jake, Bailey, Michael, Uk Hlei, Kenai, Aeran, Sean and Caleb
The test results are in and apparently all you need to complete your Year 8 addition and subtraction is a little more practice...
LI adding and subtracting decimals.
The good news is it is not that difficult if you have your standard written algorithm down, which you all do! So make sure you line up the numbers
1.97
-2.83
so that the decimal point is matching. If you have a problem like
1.97
-2.2
and you are all like "there are more numbers in the 1.97 :o", remember to transfer the place value across - as that 2.2 is also a
1.97
-2.20
With decimal problems they can go into "negative numbers", but you seem pretty confident with subtracting where the answer is less than 0, so have confidence in yourself and your knowledge.
The practice for both addition and subtraction is at the following link
Click here
Once you feel confident enough for an exit strategy so you can work on the figure it out, come to me and you will need to get 4/5 correct to show you are capable of adding and subtracting decimals.
Jaslyn, Danita, Jake, Bailey, Michael, Uk Hlei, Kenai, Aeran, Sean and Caleb
The test results are in and apparently all you need to complete your Year 8 addition and subtraction is a little more practice...
LI adding and subtracting decimals.
The good news is it is not that difficult if you have your standard written algorithm down, which you all do! So make sure you line up the numbers
1.97
-2.83
so that the decimal point is matching. If you have a problem like
1.97
-2.2
and you are all like "there are more numbers in the 1.97 :o", remember to transfer the place value across - as that 2.2 is also a
1.97
-2.20
With decimal problems they can go into "negative numbers", but you seem pretty confident with subtracting where the answer is less than 0, so have confidence in yourself and your knowledge.
The practice for both addition and subtraction is at the following link
Click here
Once you feel confident enough for an exit strategy so you can work on the figure it out, come to me and you will need to get 4/5 correct to show you are capable of adding and subtracting decimals.
Sunday, 22 September 2013
MATHS MONDAY
AMERICA’S CUP MATHS
http://www.echalk.co.uk/maths/primarynationalstrategy_yr6/dfes- mathsactivitiesforyear6/sailing.html
ENERGY + MATHS = CRAZY FUN TIMES
http://www.bbc.co.uk/bitesize/ks3/science/energy_electricity_forces/physics_triathlon/acti vity/
Force/Pressure
ENERGY + MATHS PT 2
http://www.bbc.co.uk/bitesize/ks3/science/energy_electricity_forces/energy_transfer_stora ge/activity/
http://www.echalk.co.uk/maths/primarynationalstrategy_yr6/dfes- mathsactivitiesforyear6/sailing.html
ENERGY + MATHS = CRAZY FUN TIMES
http://www.bbc.co.uk/bitesize/ks3/science/energy_electricity_forces/physics_triathlon/acti vity/
Force/Pressure
ENERGY + MATHS PT 2
http://www.bbc.co.uk/bitesize/ks3/science/energy_electricity_forces/energy_transfer_stora ge/activity/
Thursday, 19 September 2013
Monday, 16 September 2013
Factoring
LI simple factoring with algebraic equations
Okay, so the key point is that we are rearranging the terms inside the equation not getting rid of them. Basically this is not about solving the problem, finding out what the x, or a, or b actually is but condensing the equation down.
As he said you can always check it back.
Lets look through this example
Okay, so the key point is that we are rearranging the terms inside the equation not getting rid of them. Basically this is not about solving the problem, finding out what the x, or a, or b actually is but condensing the equation down.
As he said you can always check it back.
Lets look through this example
- Factor 3x – 12.
The things that are similar in the equations are, well, both numbers can be divided by 3. If you look at the 12 you know that 12 divided by 3 =4, and 3/3=1.
So factor the 3 number out to the front:
- 3x – 12 = 3( )
When I divided the "3" out of the "3x", I was left with only the "x" remaining. I'll put that "x" as my first term inside the parentheses:
3x – 12 = 3(x )
3x – 12 = 3(x – 4)
Okay try these examples
Factor 7x – 7.
Factor 8x - 16
Factor 4x - 8y
Factor 12y2 – 5y.
Once completed, bring your work up and let me have a look and then you can create a poster sharing your learning for the algebra display wall.
SOLVING LINEAR EQUATIONS
LI graphing linear equations
Morena team,
So we ran into some confusion around linear equations. Lets go back
we are going to graph this equation
y= 2x +3
Step 1. Create a three columned table like the one below.
Step 2. Start by picking your x values. In the table below you can see that the person has picked -4 all the way to 2.
Step 3. Work out what the y= by placing each of the x values into the equation. eg.
y=2x + 3
so
y= 2 times -4 and then add three. Remember in bedmas we do the multiplication first, then the addition.
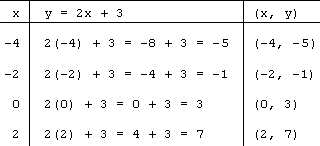
Do this for each of your x terms which you can put in your third column, which will have the coordinates for you to graph.
Lets try doing it with the equation
y= 3x +1
Remember to use the steps above.
NEXT: actually graph those points. Remember, its always going to be a straight line.
Once you have created a table like the one above with each of your terms, read through this great tutorial on graphing the points, although you guys seem pretty capable at graphing coordinates. Click here.
Morena team,
So we ran into some confusion around linear equations. Lets go back
we are going to graph this equation
y= 2x +3
Step 1. Create a three columned table like the one below.
Step 2. Start by picking your x values. In the table below you can see that the person has picked -4 all the way to 2.
Step 3. Work out what the y= by placing each of the x values into the equation. eg.
y=2x + 3
so
y= 2 times -4 and then add three. Remember in bedmas we do the multiplication first, then the addition.
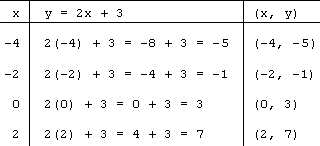
Do this for each of your x terms which you can put in your third column, which will have the coordinates for you to graph.
Lets try doing it with the equation
y= 3x +1
Remember to use the steps above.
NEXT: actually graph those points. Remember, its always going to be a straight line.
Once you have created a table like the one above with each of your terms, read through this great tutorial on graphing the points, although you guys seem pretty capable at graphing coordinates. Click here.
Wednesday, 11 September 2013
Monday, 2 September 2013
Thursday, 15 August 2013
Knife Party - Centipede (Official Video)
we have chosen this because it has a awesome starting and it sounds awesome the whole way through and it has good bass and we like it
Sunday, 11 August 2013
Friday, 26 July 2013
T3 W1 Proportions and Ratios
Proportions are not Fractions
PAINT PROBLEM
Yellow and red paint are mixed at a paint factory to make two orangy colours. The
“Raro” colour is made from mixing the 1 part yellow to 1 part red. The “Tango” is made
from mixing 1 part yellow to two parts red.
“Raro” is sold in 2 litre tins and “Tango” in 3 litre tins.
Answer these.
1) Which of the two mixes is more orange? Why?
2) What is the ratio of yellow to red in “Raro”?
3) What fraction is yellow in “Raro”?
4) What is the ratio of yellow to red in “Tango”?
5) What fraction is yellow in “Tango”?
Buddy buys a tin of each colour and mixes them both together to make 5 litres of
what he calls “Sunset”.
6) Is the new colour more or less orange than “Raro”? Explain your answer
He says the “Raro” is 1/2 yellow and the “Tango” is 1/3 yellow so adding these gives
“Sunset” a proportion of 2/5ths yellow. He says this is not how to add fractions!
7) Is Buddy correct? Is there another answer?
8) What is the ratio of yellow to red in “Sunset”?
Exactly halfway between the colour “Raro” (1:1) and “Tango” (1:2) is another colour
called “Mandarin”.
9) What is the ratio of yellow to red in “Mandarin”?
10) What is the proportion of yellow in “Mandarin”?
11) Explain how to mix 2L tins of “Raro” and 3L tins of “Tango” to make “Mandarin”
PROBLEM 2
Yellow and red paint are mixed at paint factory to make two orangy colours. The
“Raro” colour is made from mixing the 1 part yellow to 1 part red. The “Tango” is made
from mixing 1 part yellow to two parts red. “Raro” is sold in 2 litre tins and “Tango” in 2 litre tins.
(Note that the tins are the same size.)
Answer these.
1) Which of the two mixes is more orange? Why?
2) What is the ratio of yellow to red in “Raro”?
3) What proportion is yellow in “Raro”?
4) What is the ratio of yellow to red in “Tangello”?
5) What proportion is yellow in “Tangello”?
Buddy buys a tin of each colour and mixes them both together to make 4 litres of
what he calls “Bluemoon”.
6) Is the new colour more or less orange than “Raro”?
He says the “Raro” is 1/2 yellow and the “Tangello” is 1/3 yellow so adding like we add
fractions gives “Bluemoon” a proportion of 5/6ths yellow. He says this is how to add
fractions but there is not that much yellow in “Bluemoon”. Something is wrong!
7) Is Buddy correct? Is there a better answer?
8) What is the ratio of yellow to red in “Bluemoon”?
Exactly halfway between the colour “Raro” (1:1) and “Tangello” (1:2) is another colour
called “Mandarine” which Buddy says has ratio of 1:1.5 or 2:3 yellow to red.
9) Is halfway between 1:1 and 1:2 exactly 2:3? Is Buddy correct?
10) What is the proportion of yellow in “Mandarine”?
11) Explain how to mix 2l tins of “Raro” and “Tangello” to make “Mandarine”
PAINT PROBLEM ANSWERS
1) More Orange? What does this mean? Raro is in the middle so could be a ‘truer’ orange.
Tango will be a deeper orange with more red in it.
2) 1:1
3) ½
4) 1:2
5) 1/3
6) Again what does this question mean? One way to explain this is to say it has more red than
Raro (so would appear darker (more reddy) than Raro) and less red than Tango (so would
appear lighter (or more yellowy) than Tango).
7) Buddy is correct. Model this with unifix or multilink blocks, and put both lots into a
container. There is no other answer.
8) 2:3
9) Your answer to this problem should be discussed with your teacher
10) 5/12ths from the ratio 5:7 This answer comes from the discussion for question 9
11) Mixing the Mandarin is tricky with one 2L tin and one 3L tin but with multiple tins of each
it can be done! Three tins of Raro gives 3:3 and 2 tins of Tango gives 2:4. Adding this gives
us 10 litres of Mandarin mixed perfectly 5:7.
Problem 2
1) More Orange? What does this mean? Raro is half and half so could be more “orange like”.
Tangello will be a deeper reddy orange.
2) 1:1
3) 1/2
4) 1:2
5) 1/3
6) Bluemoon orange is between Raro orange and Tangello orange but more yellow than
Sunset.
7) Buddy is astute to notice he is “wrong”! He added ½ (from one yellow out of two for raro)
and 1/3 (from one yellow out of three for tangello), which is 3/6 + 2/6 = 5/6. The same
logic says that to work out the amount of red, 1/2 + 2/3 = 3/6 + 4/6 = 7/6, which is more
than in the whole paint tin! Actually, it is the amount of red in two paint tins.
If we put these together, they will give us the correct ratio of yellow to red, 5:7.
8) 5:7
9) Discuss your answer to this problem with your teacher
10) 5/12ths from the ratio 5:7
11) Mixing the Mandarine is very tricky with these 2L tins, but it can be done! 3 tins of 1:1 and
3 tins of 1:2 will give the correct mixture. This in effect creates the same size (Litre) units
and so preserves all the relationships.
PAINT PROBLEM
Yellow and red paint are mixed at a paint factory to make two orangy colours. The
“Raro” colour is made from mixing the 1 part yellow to 1 part red. The “Tango” is made
from mixing 1 part yellow to two parts red.
“Raro” is sold in 2 litre tins and “Tango” in 3 litre tins.
Answer these.
1) Which of the two mixes is more orange? Why?
2) What is the ratio of yellow to red in “Raro”?
3) What fraction is yellow in “Raro”?
4) What is the ratio of yellow to red in “Tango”?
5) What fraction is yellow in “Tango”?
Buddy buys a tin of each colour and mixes them both together to make 5 litres of
what he calls “Sunset”.
6) Is the new colour more or less orange than “Raro”? Explain your answer
He says the “Raro” is 1/2 yellow and the “Tango” is 1/3 yellow so adding these gives
“Sunset” a proportion of 2/5ths yellow. He says this is not how to add fractions!
7) Is Buddy correct? Is there another answer?
8) What is the ratio of yellow to red in “Sunset”?
Exactly halfway between the colour “Raro” (1:1) and “Tango” (1:2) is another colour
called “Mandarin”.
9) What is the ratio of yellow to red in “Mandarin”?
10) What is the proportion of yellow in “Mandarin”?
11) Explain how to mix 2L tins of “Raro” and 3L tins of “Tango” to make “Mandarin”
PROBLEM 2
Yellow and red paint are mixed at paint factory to make two orangy colours. The
“Raro” colour is made from mixing the 1 part yellow to 1 part red. The “Tango” is made
from mixing 1 part yellow to two parts red. “Raro” is sold in 2 litre tins and “Tango” in 2 litre tins.
(Note that the tins are the same size.)
Answer these.
1) Which of the two mixes is more orange? Why?
2) What is the ratio of yellow to red in “Raro”?
3) What proportion is yellow in “Raro”?
4) What is the ratio of yellow to red in “Tangello”?
5) What proportion is yellow in “Tangello”?
Buddy buys a tin of each colour and mixes them both together to make 4 litres of
what he calls “Bluemoon”.
6) Is the new colour more or less orange than “Raro”?
He says the “Raro” is 1/2 yellow and the “Tangello” is 1/3 yellow so adding like we add
fractions gives “Bluemoon” a proportion of 5/6ths yellow. He says this is how to add
fractions but there is not that much yellow in “Bluemoon”. Something is wrong!
7) Is Buddy correct? Is there a better answer?
8) What is the ratio of yellow to red in “Bluemoon”?
Exactly halfway between the colour “Raro” (1:1) and “Tangello” (1:2) is another colour
called “Mandarine” which Buddy says has ratio of 1:1.5 or 2:3 yellow to red.
9) Is halfway between 1:1 and 1:2 exactly 2:3? Is Buddy correct?
10) What is the proportion of yellow in “Mandarine”?
11) Explain how to mix 2l tins of “Raro” and “Tangello” to make “Mandarine”
PAINT PROBLEM ANSWERS
1) More Orange? What does this mean? Raro is in the middle so could be a ‘truer’ orange.
Tango will be a deeper orange with more red in it.
2) 1:1
3) ½
4) 1:2
5) 1/3
6) Again what does this question mean? One way to explain this is to say it has more red than
Raro (so would appear darker (more reddy) than Raro) and less red than Tango (so would
appear lighter (or more yellowy) than Tango).
7) Buddy is correct. Model this with unifix or multilink blocks, and put both lots into a
container. There is no other answer.
8) 2:3
9) Your answer to this problem should be discussed with your teacher
10) 5/12ths from the ratio 5:7 This answer comes from the discussion for question 9
11) Mixing the Mandarin is tricky with one 2L tin and one 3L tin but with multiple tins of each
it can be done! Three tins of Raro gives 3:3 and 2 tins of Tango gives 2:4. Adding this gives
us 10 litres of Mandarin mixed perfectly 5:7.
Problem 2
1) More Orange? What does this mean? Raro is half and half so could be more “orange like”.
Tangello will be a deeper reddy orange.
2) 1:1
3) 1/2
4) 1:2
5) 1/3
6) Bluemoon orange is between Raro orange and Tangello orange but more yellow than
Sunset.
7) Buddy is astute to notice he is “wrong”! He added ½ (from one yellow out of two for raro)
and 1/3 (from one yellow out of three for tangello), which is 3/6 + 2/6 = 5/6. The same
logic says that to work out the amount of red, 1/2 + 2/3 = 3/6 + 4/6 = 7/6, which is more
than in the whole paint tin! Actually, it is the amount of red in two paint tins.
If we put these together, they will give us the correct ratio of yellow to red, 5:7.
8) 5:7
9) Discuss your answer to this problem with your teacher
10) 5/12ths from the ratio 5:7
11) Mixing the Mandarine is very tricky with these 2L tins, but it can be done! 3 tins of 1:1 and
3 tins of 1:2 will give the correct mixture. This in effect creates the same size (Litre) units
and so preserves all the relationships.
Wednesday, 19 June 2013
Saturday, 15 June 2013
PYTHAGORANS WEEK 7
MONDAY
Open ended maths question to start the week
These crime statistics are nationwide, not just Nelson.
(Just in case you are wondering "where is the maths in this Mr Phillips", your ability to analyse data and come up with conclusions about that data is at the essence of Mathematics. It is the same as working out 4x7= 28, because you have identified the data and made some informed strategic thinking to get the answer.)
LEARNING INTENTION
To use compensation from tidy numbers to help me solve division problems
TUESDAY
LEARNING INTENTION
I am learning to use compensation from tidy numbers to help me solve division problems
LEARNING INTENTION
to use reversibility to help me solve division problems
Okay and just for a change of scene, try these Khan Academy division exercises with remainders
CLICK HERE
If you get stuck watch the video below
Then try this
LINK RIGHT HERE
I don't know if you guys know about the scratchpad, but it is really great and will make your working a whole heap easier on the khan academy
Its down the bottom of the page
Where it says "show scratchpad", will make a bit of a difference with your working out of these problems!
Open ended maths question to start the week
These crime statistics are nationwide, not just Nelson.
(Just in case you are wondering "where is the maths in this Mr Phillips", your ability to analyse data and come up with conclusions about that data is at the essence of Mathematics. It is the same as working out 4x7= 28, because you have identified the data and made some informed strategic thinking to get the answer.)
LEARNING INTENTION
To use compensation from tidy numbers to help me solve division problems
TUESDAY
LEARNING INTENTION
I am learning to use compensation from tidy numbers to help me solve division problems
LEARNING INTENTION
to use reversibility to help me solve division problems
Okay and just for a change of scene, try these Khan Academy division exercises with remainders
CLICK HERE
If you get stuck watch the video below
Then try this
LINK RIGHT HERE
I don't know if you guys know about the scratchpad, but it is really great and will make your working a whole heap easier on the khan academy
Its down the bottom of the page
Where it says "show scratchpad", will make a bit of a difference with your working out of these problems!
EUKLIDS WEEK 7
EUKLIDS
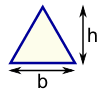 | Triangle Area = ½ × b × h b = base h = vertical height | 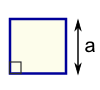 | Square Area = a2 a = length of side | |
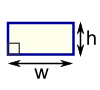 | Rectangle Area = w × h w = width h = height | 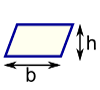 | Parallelogram Area = b × h b = base h = vertical height | |
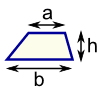 | Trapezoid (US) Trapezium (UK) Area = ½(a+b) × h h = vertical height |  | Circle Area = π × r2 Circumference = 2 × π × r r = radius | |
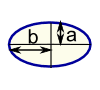 | Ellipse Area = πab | 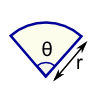 | Sector Area = ½ × r2 × θ r = radius θ = angle in radians |
You will need to write out these formulas in your books as it will really help when you are solving the equations.
Test your ability!!!!!!
(For some of the problems, especially those using π (the greek letter Pi which is the ratio of a circles circumference to its diameter or θ (the greek letter Theta which represents an angle)
Geometry, what a blast.
Thursday, 13 June 2013
EUKLIDS FRIDAY
Euklids
To multiply decimal numbers:
- Multiply the numbers just as if they were whole numbers.
- Line up the numbers on the right - do not align the decimal points.
- Starting on the right, multiply each digit in the top number by each digit in the bottom number, just as with whole numbers.
- Add the products.
- Place the decimal point in the answer by starting at the right and moving a number of places equal to the sum of the decimal places in both numbers multiplied.

See how it moves three places across because in the question there were three decimals places 2.77 has two and 2.8 has one.
37.7 x 2.8 =
3.77x2.8=
3.77x 28=
3.77 x 0.28=
Try these easy ones first
|
|
|
|
|
|
|
|
|
|
Tuesday, 4 June 2013
hypatias week 6
Why not give this a try and see if you can work out
8x8=
9x7=
9x6=
Did this method help?
Okay we are going to use the strategy compensation to solve multiplication problems
And we'll quickly revise
LEARNING INTENTION
to identify place value in numbers that involve decimals
Decimal Place Value: Decimal Place Value
So what is the place value of 5 in the number
654.213?
What is the place value of 1 in the number
654.213?
What is the place value of 7 in the number
845.769?
What is the place value of 9 in the number
845.769?
Please write down the questions in your books.
Once you have completed this, write down the two numbers in word form. If you are unsure of how to do this, have a watch of this resource.
FRIDAY
LEARNING INTENTION
Put decimals on a number line
This is a quick warm up and a quick refresher of things you have already learnt.
Spend five minutes practising on THIS LINK
Points on a number line: Points on a number line
Okay now try it for yourself
draw this number line into your book
Make sure there is an even space between each of the numbers on your number line.
Place the following numbers on the number line. If you get stuck, refer back to the video.
0.5, 2 1/4 , -4.3 , 3.9
Once you have completed this number line, show it to MR PHILLIPS and then you can continue on your xtramaths
Multiply
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Subscribe to:
Comments (Atom)
































